În urma reacțiilor cititorilor interesați, unele corecte și consistente, revin cu precizări în legătură cu problema de fizică propusă.
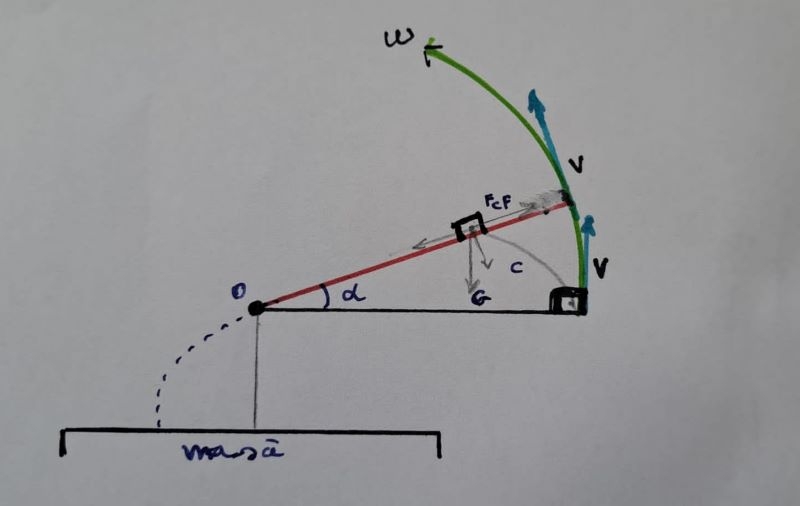
Deci, avem o bară plată, de lungime R, la capătul căreia este așezat un cubuleț. Bara se rotește în plan vertical (nu în plan orizontal, cum au înțeles unii cititori, caz în care, funcție de mărimea vitezei de rotație, fie cubulețul rămâne pe bară, rotindu-se solidar cu ea, și problema nu mai există, fie cade liber de pe bară, și problema devine banală), în sens invers acelor de ceasornic, cu viteza constantă v, respectiv viteza unghiulară Ω. O observație corectă este că, dacă bara pleacă din poziție orizontală, din repaus, atunci trebuie să descrie o mișcare circulară neuniformă, cu accelerație, pentru a ajunge de la viteza 0 la viteza v. Asta complică problema (apare accelerația Euler), care oricum nu e simplă, așa că vom considera, pentru început, că bara se află practic instantaneu în mișcare cu viteza v, plecând de la orizontală (tehnic, asta se poate realiza cu un cuplaj electromagnetic între cubuleț și bară, presupuse metalice, cuplaj care să fie anulat brusc, printr-un întrerupător, când bara aflată în rotație cu viteza v ajunge în poziție orizontal-dreapta).
Asupra cubulețului se exercită forța centrifugă Fcf și atracția gravitațională G (mai e și forța Coriolis, dar o neglijăm). Dacă viteza de rotație v este mare față de greutatea cubulețului, atunci el poate fi aruncat de la bun început de pe bară, pe o traiectorie tangentă (ca dintr-o catapultă). Dacă v este relativ mică, atunci componenta în lungul barei a greutății G poate fi echilibrată de Fcf (neglijăm frecarea între cubuleț și bară), adică, Fcf=G sin α → mv2/R=mg sin α → sin α = v2/Rg → α = arcsin v2/Rg, unghiul de la care încolo cubulețul începe să alunece pe bară spre centrul de rotație. Ei, și aici începe dansul.
Cubulețul alunecă pe bară, care se rotește. Asta înseamnă că unghiul α crește continuu. Prin urmare, am avea o problemă clasică de plan înclinat, cu deosebirea că unghiul planului este variabil. Deci, componenta în lungul barei a accelerației gravitaționale, g sin α, nu este constantă, ea crește – avem o accelerație a accelerației, o derivată a doua a vitezei sau o derivată a treia a spațiului.
Mai mult, cubulețul deplasându-se în jos pe bară, își schimbă continuu raza de rotație, care devine din ce în ce mai mică. Prin urmare, accelerația centrifugă v2/R este și ea variabilă – cu cât raza scade, accelerația crește. Studiind mișcarea cubulețului sub acțiunea acestor două forțe variabile, Fcf și G sin α (în problemele clasice ele sunt constante) trebuie să calculăm viteza cubulețului când ajunge în centrul de rotație O, precum și unghiul barei față de orizontală în acel moment. Cu aceste două date, vO și α, avem o problemă clasică de aruncare în câmp gravitațional a unui corp sub un unghi, cu viteză inițială. Dar trebuie să le aflăm...
În ce privește traiectoria în spațiu (ștergem mental bara) a cubulețului, ea este o curbă c, rezultată din compunerea unei mișcări de rotație, cea a barei, cu o mișcare rectilinie neuniformă, cea a cubulețului în lungul barei. Spor la raționat!
Apăsați pe imagine pentru a o vizualiza la rezoluție completă.
Urmăriți Republica pe Google News
Urmăriți Republica pe Threads
Urmăriți Republica pe canalul de WhatsApp





