Rezolvați această problemă: Într-un sac, se află 24 de bile de marmură – unele albe și unele negre. Din sac, este scoasă la întâmplare o bilă, căreia i se notează culoarea și este pusă înapoi...

Foto: DPA Alliance/ Alamy/ Profimedia

La ultima ediție a testelor TIMSS, elevii români de clasa a opta au obținut un scor mediu de 479 de puncte la matematică, situându-se pe ultimul loc din UE. 

Testul pe care l-au dat a evaluat performanțele elevilor la patru capitole – numerație, algebră, geometrie și date și probabilități. Elevii români au obținut cel mai bun scor la algebră – cu 11 puncte peste media țării, și cel mai slab la capitolul date și probabilități – cu 21 de puncte sub medie.

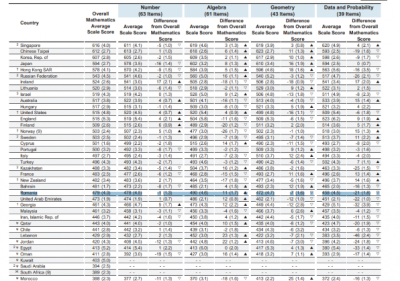
La problemele de nivel ridicat, elevii români au întâmpinat dificultăți mai serioase decât majoritatea celor din străinătate. Iată un exemplu, la care media internațională a răspunsurilor a fost de 43 din 100, în timp ce în România media a fost de 30 din 100.

„Într-un sac, se află 24 de bile de marmură – unele albe și unele negre. Din sac, este scoasă la întâmplare o bilă, căreia i se notează culoarea și este pusă înapoi. Acest lucru este făcut de 120 de ori, iar o bilă albă apare de de 70 de ori. Câte bile albe este probabil să se afle în sac?”

Conform noii programe la matematică, elevii de clasa a VIII-a trebuie să studieze domeniul de conținut organizarea datelor, probabilități și elemente de statistică matematică. Însă copiilor li se predau mai multe elemente de statistică descriptivă, care presupun un grad de abstractizare ridicat și pe care un elev obișnuit de gimnaziu nu le întâlnește cu ușurință în lumea reală, și mai puține elemente de probabilități, care să plece de la situații ușor de întâlnit. Au existat elemente de statistică și probabilități și în vechea programă de gimnaziu, dar foarte puține. În clasa a VI-a probabilitățile erau folosite pentru a exemplifica rapoarte. Iar în clasa a VII-a erau prezentate câteva elemente de organizare a datelor.

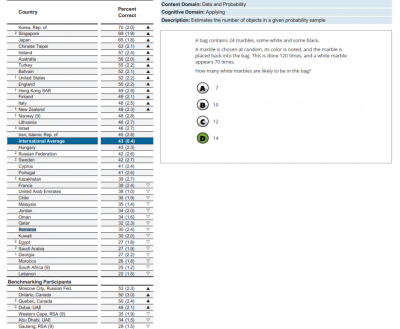
Elemente de statistică. Indicatorii tendinței centrale (frecvență, medie, mediană, mod și amplitudinea unui set de date) – acesta este titlul capitolului în Manualul de matematică de clasa a VIII-a, realizat de Editura Intuitext, unul dintre cele 3 aprobate de Ministerul Educației, care corespunde domeniului de conținut mai sus amintit. Capitolul pleacă de la un exemplu care are legătură cu viața reală: lista vânzărilor de bilete ale unei companii de transport ( care au costuri diferite), făcute într-un interval de 10 minute. Elevilor li se cere să afle care a fost cel mai vândut produs, care este numărul tranzacțiilor făcute și care este, potrivit probabilităților, următorul bilet vândut după expirarea intervalului de timp dat. Apoi trece la teorie:

• „Frecvența este un număr care ne arată de câte ori se repetă o valoare numerică într-un set de date. 
• Modul unui set de date este valoarea numerică cu frecvența cea mai mare, dacă aceasta există.
• Dacă mai multe valori numerice au aceeași frecvență spunem că setul de date are mai multe valori modale.
• Dacă toate valorile numerice au aceeași frecvență spunem că setul de date nu conține valori modale.
• Modul unui set de date ne arată caracteristica cu cea mai mare probabilitate de realizare.”

În sistemul de educație din Germania, probabilitățile sunt predate cu ajutorul abordării constructiviste (la fel ca celelalte teme), care pleacă de la cunoașterea anterioară a elevilor și care îi stimulează ca pe baza acesteia să ajungă la cunoștințe noi. Deși exemplele date inițial și întrebările puse la început copiilor par simple, ele pun bazele înțelegerii unor noțiuni din ce în ce mai avansate și rezolvării unor probleme din ce în ce mai complexe. Și, cel mai important, activând și folosind cu pricepere ceea ce elevul cunoștea deja. La ultima ediție a testării TIMSS, nu au participat și elevi germani de clasa a VIII-a, pentru a putea face o comparație cu scorul României, ci doar elevi de clasa a IV-a. Pe de altă parte, din România, au participat doar elevii de clasa a VIII-a.

În manualul de clasa a VIII-a, realizat de editura Ernst Klett Verlag și utilizat în landul Baden-Württemberg din Germania, lecția debutează cu o întrebare care declanșează un conflict cognitiv. Să presupunem că ați putea juca oricare dintre cele trei jocuri de noroc din imaginea de mai jos.

Pe care l-ați alege pentru a avea șanse mari de a nimeri mai frecvent 6?

La Roata Norocului, probabilitate de a obține un 6 este de 2 din 5. La extragerea bilelor, probabilitatea este de 5 din 9, iar la aruncarea zarului de 1 din 6. Prin urmare, cel mai bine ar fi să alegeți al doilea joc.

Apoi manualul îi poartă pe elevi într-o discuție mai amănunțită pe baza unor exemple concrete, ușor de înțeles.

Avem un bol cu bile pare și impare colorate diferit. Care este probabilitatea de a extrage o bilă cu un număr par?

Avem un zar cu 6 fețe. Care este probabilitatea de a cădea după aruncare pe una dintre ele?

Însă ce se întâmplă dacă zarul are forma unui tetraedru, așadar are doar 4 fețe? Care e probabilitatea de a cădea pe fața cu numărul 3 de exemplu?

Dar dacă are 20?

Însă ce se întâmplă dacă zarul are forma unui tetraedru, așadar are doar 4 fețe? Care e probabilitatea de a cădea pe fața cu numărul 3 de exemplu?

Dar dacă are 20?

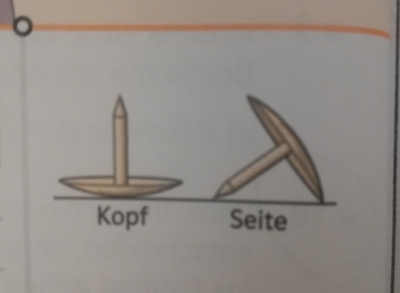
Se trece apoi la al doilea exemplu de acest tip. Care este probabilitatea ca pioneza să cadă cu acul în sus și care este probabilitatea să cadă cu acul într-o parte?

După un număr mare de aruncări cu acest zar, se observă că probabilitățile ca acesta să cadă pe fața cu numărul 1 este egală cu probabilitatea ca el să cadă pe fața cu numărul 5 – 33,5%. La fel, probabilitățile ca el să cadă pe fețele cu numerele 2, 3 și 4 sunt egale – 11%.

În manualul scrie că trebuie făcute multe aruncări ale pionezei. Astfel, sunt aduse în prim plan rezultatele a trei serii de câte 500 de aruncări și un grafic din care se poate vedea cum evoluează probabilitatea ca pioneza să cadă cu vârful în sus (axa Oy) în funcție de numărul de aruncări (sunt pe axa Ox).

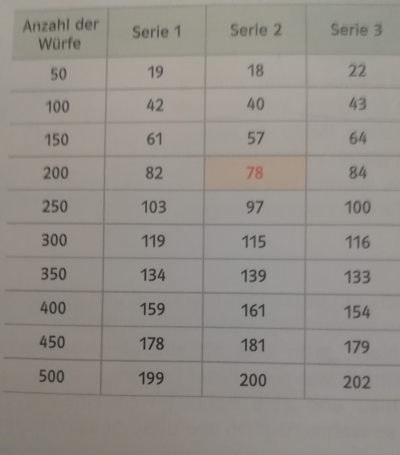
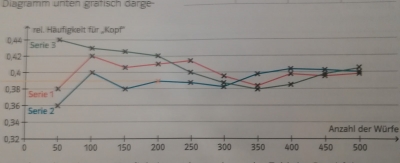
Graficul ne indică următorul lucru: cu cât crește numărul de aruncări, cu atât ne apropiem mai mult de valoarea 0,4. Acest lucru este valabil pentru fiecare din cele 3 serii de aruncări. Reformulând, probabilitatea ca pioneza să cadă cu vârful în sus este de 40%.

După ce se discută pe marginea experimentului de mai sus, este introdusă legea empirică a numerelor mari: dacă un experiment aleatoriu este repetat de foarte multe ori, atunci frecvențele relative ale unui rezultat se abat tot mai puțin în raport cu o anumită valoare, care este considerată a fi probabilitatea acelui rezultat.

Tot la lecția despre probabilități, în același manual, elevilor li se înfățișează un cadran în trei culori cu o săgeată care se poate roti, ca la Roata Norocului.

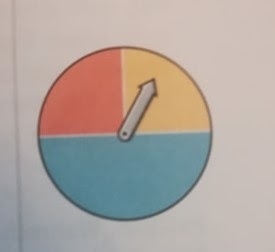
Apoi elevii sunt întrebați care este probabilitatea ca săgeata să ajungă pe roșu (1/4), care este probabilitatea ca ea să ajungă pe galben (1/4) și care este probabilitatea ca ea să ajungă pe albastru (1/2). Folosirea cercului împărțit în cadrane este o modalitate simplă și eficientă prin care copiii pot să înțeleagă intuitiv ce înseamnă probabilitățile inegale.

Ulterior, lucrurile devin ceva mai complicate – elevii sunt întrebați care este probabilitatea ca săgeata să ajungă de două ori consecutiv pe aceeași culoare de exemplu (roșu, albastru sau galben).

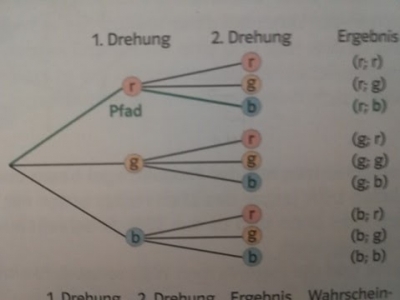
Doar după ce elevii și-au bătut capul, li se arată o modalitate de a face calculele. Dar este foarte probabil să descopere și singuri această soluție.

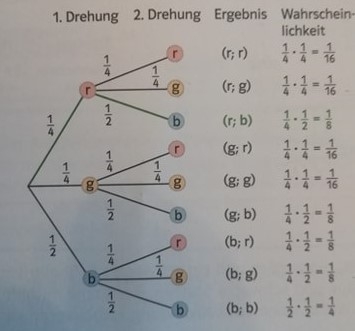
Această reprezentare este suficient de intuitivă pentru a fi înțeleasă și de către elevii de nivel mediu, care au o capacitate mai redusă de abstractizare.

Chiar dacă nu vei ajunge niciodată statistician, probabilitățile sunt folositoare în viața reală pentru că te pot ajuta să estimezi rezultatul unei acțiuni pe care vrei să o întreprinzi, riscurile sau piedicile pe care le-ai putea întâmpina. Aceste lucruri pot pleca de la simpla estimare a timpului de care ai nevoie pentru a ajunge undeva, în funcție de probabilitatea de a întâlni în cale semafoare pe verde, și poate ajunge la decizii complexe de viață.

Pentru partea cu semafoarele, te pregătește un exercițiu din manual.

O persoană întâlnește 2 semafoare în drumul spre serviciu. Știe că la fiecare din ele este o probabilitate de 50% să-l prindă pe verde. El trage concluzia că 100% va prinde verde măcar la unul din semafoare. Elevii sunt puși să-și spună părerea despre presupunerea acestuia. De fapt, probabilitatea este de 75%.

Dacă se folosesc exemple precum cele de mai sus, este mai potrivit ca elevii să intre mai întâi în contact cu probabilitățile, nu cu elementele de statistică. Pentru că ei întâlnesc multe situații în viața reală care pot fi abordate/ înțelese cu ajutorul probabilităților. Elementele de statistică sunt utile dacă fac măsurători repetate, experimente de laborator etc. Or, puțini dintre elevi au avut astfel de experiențe până în clasa a VIII-a. Și chiar dacă se fac în școală elemente de statistică, ele ar fi mai ușor de înțeles de elevi dacă ar face în prealabil și probabilități.

Articol publicat pe blogul Centrului de Evaluare și Analize Educaționale.

Urmăriți Republica pe Google News

Urmăriți Republica pe Threads

Urmăriți Republica pe canalul de WhatsApp